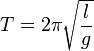.....CI SONO ANCHE LORO!!!!!!

OMINAZIONE

L'insieme degli eventi attraverso cui si è compiuta l'evoluzione della specie umana viene detto ominazione.

Topo? No, lemure!

Le prime tappe dell'ominazione si svolsero in Africa. Tradizionalmente si fa iniziare l'ominazione circa  70 milioni di anni fa, quando dai mammiferi si svilupparono i primati, l'ordine al quale appartiene l'uomo. Il termine “primati” compare per la prima volta nel XVIII secolo, nelle opere del naturalista svedese Carlo Linneo, secondo il quale i primati costituivano un ordine comprendente scimmie, proscimmie. Il termine è rimasto nell’attuale nomenclatura zoologica per designare l’ordine di mammiferi comprendente le forme del regno animale più simili all'uomo, come le scimmie e le scimmie antropomorfe. I primati ebbero origine tra il Paleocene e l'’Eocene e si presume che si siano evoluti da animali simili agli insettivori. I primati originari erano animali notturni, arboricoli, con mani e piedi prensili, muso piatto; gli occhi erano grandi e frontali e consentivano una visione stereoscopica (percezione della profondità), si presume che fossero simili agli attuali lemuri. Progressivamente alcuni primati divennero diurni, acquisirono la capacità di vedere i colori e per spostarsi da un ramo all'altro adottarono la brachiazione. Questo metodo di locomozione, che consiste nel tenersi sospeso con le braccia, comportò delle modifiche a livello della colonna vertebrale e del bacino, che consentirono la successiva evoluzione della stazione eretta, tipica dell'uomo.

A circa 20 milioni di anni fa risale un gruppo di primati, le Driopitecine, con caratteri umanoidi, ma vita ancora arboricola. Dalle Driopitecine derivarono le Ramapitecine, vissute da 14 a 8 milioni di anni fa. La loro comparsa avvenne quando un lungo periodo freddo determinò il ritiro della foresta tropicale e lo sviluppo di savane, un tipo di vegetazione che male si accorda con la vita arboricola. In effetti, la dentatura delle Ramapitecine rivela un parziale adattamento alla vita al suolo, per cui  nella dieta sono introdotti semi, tuberi, radici.

  La comparsa degli ominidi

Lucy

Si definiscono ominidi i progenitori dell'uomo con stazione eretta e locomozione bipede. I primi ominidi appartengono al genere Australopithecus e i loro resti fossili sono stati trovati in Tanzania e in Etiopia. Essendo bipede, Australopithecus non aveva necessità di impiegare l'arto superiore per la locomozione; questo poté allora perfezionarsi nella manipolazione e nella presa di oggetti. Gli Australopithecus comparvero attorno a 4,4 milioni di anni fa con la specie A. ramidus, della quale conserviamo solo alcuni denti. Di un'altra specie, A. afarensis, è stato scoperto nel 1974 lo scheletro quasi completo di una femmina, che è stata battezzata dagli scopritori Lucy. ( Guarda il video)

Circa 2 milioni di anni fa, da qualche popolazione di un'altra specie, A. africanus, ebbe origine Homo abilis, capace di produrre rudimentali utensili in pietra scheggiata.

Da H. abilis derivò Homo erectus (1,8 milioni di anni fa), più progredito nella fabbricazione degli utensili. H. erectus si spostò dalle originarie terre africane in Eurasia; imparò a utilizzare il fuoco per scaldarsi e forse per cuocere, a cacciare grandi animali, a stabilirsi in accampamenti. Sviluppò il linguaggio, che favorì l'organizzazione degli uomini in tribù.

 L'uomo attuale

Circa 200.000 anni fa H. erectus venne gradualmente sostituito da Homo sapiens.

Uomo di Neanderthal

In Europa, in seguito a migrazioni dall'Africa, l'homo erectus di differenziò in homo neanderthalensis   o uomo di Neanderthal. Egli viveva  in tribù meglio strutturate; si curava  degli  gli anziani e seppelliva  i morti; adottava  forse anche  pratiche rituali.
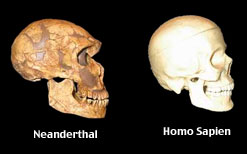Probabilmente 35000 anni fa l'uomo di Neanderthal, a causa  del clima rigido delle glaciazioni, si estinse e lo sostituì, o assorbì ,tramite successivi  incroci, l'Homo sapiens sapiens. A questo genere appartengono tutti gli uomini viventi oggi sulla terra. I più antichi resti fossili di Homo sapiens sono di 35000 anni fa; (in Europa, dalla località del ritrovamento, si chiama uomo di Cro-Magnon). Con la comparsa dell’Homo. sapiens assume maggiore peso l'evoluzione culturale: si acquisiscono tecniche più perfezionate di caccia e guerra, compaiono manifestazioni grafiche (pitture e graffiti ritrovati nelle grotte che servivano da abitazione) e oggetti scolpiti con valore magico-rituale. Vengono addomesticati gli animali e si sviluppa l'agricoltura.

Homo sapiens sapiens

  

Vediamo anche questa animazione che ci riassume in  circa sei minuti la storia della terra e dell'uomo.

AMMINOACIDI E PROTEINE

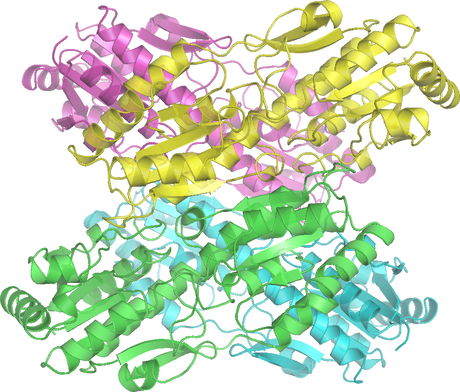
Le proteine o protidi sono il componente principale di tutte le cellule dei viventi. Secondo alcune stime, nell'uomo ci sono circa 100.000 proteine diverse. Esse svolgono la maggior parte delle funzioni vitali: costituiscono infatti gli enzimi, che presiedono a tutte le trasformazioni chimiche delle cellule; svolgono diverse funzioni strutturali, sono responsabili del movimento e della contrazione muscolare, presiedono a tutti i fenomeni di trasporto (l'emoglobina trasporta l'ossigeno e l'anidride carbonica in tutti i distretti dell'organismo), e svolgono ruoli importantissimi nella difesa dell'organismo da agenti estranei.

Ma cosa sono esattamente le proteine? Come sono fatte? 

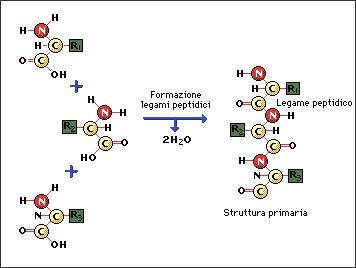
Una proteina è una catena costituita da molecole organiche di piccole dimensioni chiamate aminoacidi. Tutte le proteine conosciute sono formate dalla combinazione di soli 20 tipi di aminoacidi. Ogni aminoacido ha un atomo centrale di carbonio, che è conosciuto come carbonio alfa. All'atomo centrale sono legati un atomo di idrogeno, un gruppo amminico (NH2), un gruppo carbossilico (COOH) e una catena laterale. E' la catena laterale che distingue un aminoacido da un altro. Le catene laterali possono essere semplici come un atomo di idrogeno o complicate come due anelli di carbonio.

In una proteina, gli aminoacidi sono legati attraverso un legame, detto  legame peptidico. Le combinazioni pressoché infinite in cui si possono allineare gli aminoacidi e la forma contribuiscono a spiegare la grande diversità di compiti svolti dalle proteine negli organismi viventi.

Sono definiti essenziali quegli aminoacidi che l'organismo umano non riesce a sintetizzare in quantità sufficiente a far fronte ai propri bisogni.

Per l'adulto sono otto e più precisamente: fenilalanina, isoleucina, lisina, leucina, metionina, treonina, triptofano e valina.

Durante il periodo dell'accrescimento agli otto ricordati ne va aggiunto un nono, l'istidina. In questo periodo della vita le richieste di tale aminoacido sono infatti più elevate della capacità di sintesi endogena.

Aminoacidi essenziali nella dieta

La dieta di un individuo dovrebbe fornire tutti gli aminoacidi essenziali.

In natura esistono alimenti che contengono quantitativi sufficienti di tutti gli aminoacidi essenziali. Si parla in questo caso di proteine nobili o complete, generalmente presenti in carni, uova, pesce e latticini.

Alcuni cibi si caratterizzano invece per una deficienza "assoluta" o "relativa" di aminoacidi essenziali. Si parla in questo caso di proteine incomplete, generalmente presenti negli alimenti di origine vegetale.

Le proteine dei cereali, ad esempio, hanno deficienza relativa in alcuni aminoacidi,come lisina e triptofano.

I legumi, alimenti vegetali ricchissimi di proteine, contengono buone quantità di lisina ma sono carenti in metionina.

Anche carne, latticini e uova contengono un aminoacido limitante (generalmente metionina o triptofano). La sua concentrazione raggiunge tuttavia livelli sufficienti per garantire l'ottimale svolgimento della sintesi proteica.

Un'integrazione di cereali e legumi, in quantità opportuna, costituisce un complesso proteico ben equilibrato in grado di coprire il fabbisogno di aminoacidi essenziali. 

SCOMPOSIZIONE IN FATTORI PRIMI

Ragazzi di prima, ho trovato proprio adesso questa risorsa, dedicata a tutti coloro che hanno difficoltà nella scomposizione in fattori primi.
Andate qui, vi potreste anche divertire!!!!
Vi consiglio anche di farvi una bella passeggiata nel sito, ci sono cose molto carine, utili, interessanti! ( Ad es. dei video in inglese sulla matematica, che mi hanno fatto venire un'idea! Provate ad indovinare quale!)

PARLIAMOCI CHIARO!!!!!!!!!! DIMMI CHI SEI!!!!!!!

Dal blog  http://papillevagabonde.blogspot.it/2009/09/acidi-grassi-trans-tfa-pericolosi-per.html 
tante informazioni utili sugli acidi grassi trans, su come riconoscerli in etichetta, come evitarli

OCCHIO ALL'ETICHETTA!

Gli effetti negativi sulla salute degli acidi grassi trans ( Trans Fatty Acids TFA) sono noti già da una ventina di  anni; essi sono meglio conosciuti come oli vegetali idrogenati e sono utilizzati dall'industria alimentare perché hanno un basso costo, migliorano la consistenza del prodotto, permettono di aumentarne la durata di conservazione.

Non esistono valori limite a livello comunitario, ma molti paesi hanno ultimamente  emanato norme che in qualche modo ne limitano l'uso. Il primo paese ad adottare delle misure restrittive è stata la Danimarca nel 2003 (non possono essere più del 2%, ), negli Stati Uniti dal 2006 devono essere indicati in etichetta, nel 2008 sono vietati nei ristoranti di New York, recentemente l’Austria ne ha limitato l’uso, al si sotto del 2%. 

Ma in quali alimenti si trovano?In molti prodotti industriali come brioche, pane, dolci per la prima colazione,  pizze già pronte, nei prodotti di pasticceria, paste già pronte arrotolate, biscotti, margarine, salse, patatine surgelate da friggere, grissini, crackers.

Le principali conseguenze sulla salute umana degli acidi grassi trans sono l’infarto ( aumentano il tasso di colesterolo "cattivo"), il cancro, il sovrappeso.

Gli gli acidi grassi trans possono essere anche di origine animale, ma in questo caso non  non diminuiscono le proteine HDL (colesterolo buono, per intenderci); si  trovano nel burro, formaggio, carne, latte, pesce, frutta secca.

Leggendo le etichette si troverà scritto:

• grassi idrogenati 
• grassi parzialmente idrogenati
• oli vegetali parzialmente idrogenati
• oli vegetali idrogenati
• grassi vegetali idrogenati

Attenzione però alla scritta in etichetta "oli vegetali o grassi non idrogenati": può trarre in inganno !!!!!Vorremmo sapere:

1)Quali sono???? 

2) Sono forse gli oli di palma o di cocco che contengono una percentuale di grassi saturi piuttosto alta?

3) Se troviamo scritto grassi vegali non va bene, perchè il grasso vegetale, se non è idrogenato, si ottiene tramite frazionamento, che porta a  un concentrato di grassi saturi!

4) Apprezziamo quelle ditte che scrivono chiaramente: " contiene olio di palma". Almeno non vogliono trarre in inganno, anche se molti non leggono l'etichetta o non sanno che l'olio di palma contiene grassi saturi.

GRASSI IDROGENATI E GRASSI TRANS

da: http://www.my-personaltrainer.it/alimentazione/grassi-idrogenati.html

Idrogenazione: a cosa serve?

L'idrogenazione è un processo chimico utile alla saturazione (di solito parziale) di acidi grassi naturalmente polinsaturi; gli acidi grassi polinsaturi hanno anche doppi legami tra gli atomi di carbonio

della catena, di conseguenza vincolano meno ioni idrogeno rispetto ad un acido grasso saturo.

L'idrogenazione consiste nella semplificazione dei doppi legami a legami singoli, aumentando così la quantità di ioni idrogeno e la saturazione. All'aumentare di quest'ultima caratteristica chimica aumenta anche la solidità del prodotto; di conseguenza, grazie al processo di idrogenazione, è possibile trasformare un olio (liquido a temperatura ambiente) in un grasso solido o semisolido.

I grassi idrogenati trovano grande applicazione nella preparazione industriale dei prodotti da forno,  nella composizione delle margarine, nei gelati .

gelato e margarina

Infatti i grassi idrogenati danno plascicità al prodotto nella lavorazione ( sono solidi come i saturi!) e lo rendono friabile, cose che in passato venivano ottenute con  i grassi saturi animali (burro, strutto, sego e lardo). Oggi i grassi idrogenati hanno sostituito quasi totalmente i lipidi animali saturi per questi motivi

• minor costo
• maggiore specificità d'impiego
• maggiore stabilità termica
• maggiore stabilità organolettica
• maggiore conservabilità.

Grassi idrogenati e salute

I grassi idrogenati non sono componenti nutrizionali essenziali o utili al funzionamento dell'organismo; metabolicamente, si comportano esattamente come gli acidi grassi saturi animali svolgendo un ruolo iper-colesterolemizzante.

Essi hanno anche un altro potenziale nocivo: la presenza di acidi grassi trans.

Spesso, durante il processo di idrogenazione, la saturazione fallisce ma la struttura dell'acido grasso subisce comunque un'alterazione significativa; si tratta di una conversione geometrica molecolare da cis a trans che ne modifica le funzioni ed il metabolismo all'interno del corpo umano. E' pur vero che i grassi idrogenati non sono l'unica fonte di acidi trans, i quali si possono trovare anche tra i lipidi della carne di pecora, di bue e nei prodotti caseari; la molecola trans maggiormente presente in natura è l'acido elaidico, che corrisponde al cis-oleico, ma rispetto agli acidi grassi saturi o idrogenati in forma cis, gli acidi grassi trans favoriscono ancor di più l'innalzamento del colesterolo.

Una dieta ricca di acidi grassi trans può rappresentare un fattore di rischio per complicanze cardio-vascolari; pertanto, l'utilizzo di margarine o grassi idrogenati in sostituzione ai lipidi animali non è da considerarsi una scelta alimentare del tutto corretta.

Gli acidi grassi trans si formano anche sottoponendo gli oli ad alte temperature, quindi la frittura porta sempre alla formazione di grassi trans. Friggendo più volte con lo stesso olio si ha un bel concentrato di trans!!!! Quindi, patatine sì, ma con moderazione!E con olio buono.....( da Mc Donald friggono innumerevoli volte con grasso vegetale!!!!!!!!!!)

LABORATORIO: MISURE SUL PENDOLO

IL PENDOLO E LE SUE GRANDEZZE 
( Esperienza di laboratorio della classe III A)

UN ESPERIMENTO ALLA RICERCA DELLE FUNZIONI

CHE COLLEGANO TRA LORO LE GRANDEZZE RILEVABILI IN UN PENDOLO

  Per poter iniziare il lavoro bisogna conoscere:

 concetto di grandezza

 capacità di trovare nel piano cartesiano ogni punto corrispondente a delle coordinate date

 una certa conoscenza del concetto di funzione, con particolare riguardo ai concetti di grandezze direttamente e inversamente proporzionali.

 rappresentazioni di funzioni nel piano cartesiano

 capacità di misurare in gradi l’ampiezza di un angolo

 conoscenza della misura del tempo in minuti e secondi, e capacità di misurare intervalli di tempo di       10-30 secondi

 capacità di misurare le lunghezze

 possedere il concetto di baricentro.

Materiali

Una delle caratteristiche positive di questo lavoro è la semplicità dei materiali necessari. Naturalmente operare in condizioni di “laboratorio povero” comporta la perdita di un certo grado di precisione, ma ciò non ha impedito di lavorare in modo rigorosamente scientifico.
In ogni caso il grado di precisione ottenibile con gli strumenti utilizzati è largamente sufficiente per permettere la scoperta della legge del pendolo semplice.

Ogni gruppo dispone di:
 un filo sottile (non spago) lungo un paio di metri
 normale materiale di cancelleria, scotch compreso
 righello, squadra, goniometro e una riga da almeno 50cm
 orologio con contasecondi
 una serie di 4-5 pesi uguali, per esempio batterie stilo, monete grandi, bulloni uguali, ecc

Scopo scientifico del lavoro

Si tratta di vedere quali tra le grandezze del pendolo sono tra loro interconnesse, cioè quali sono una in funzione dell’altra e quindi dipendenti.

Le quattro grandezze che abbiamo deciso di osservare sono: tempo di oscillazione,  angolo di oscillazione, peso (massa), lunghezza del pendolo.

Abbiamo scartato le altre possibilità (temperatura, velocità, distanza tra i due punti morti, ecc) per la notevole difficoltà di rilevare o di calcolare dati relativi a queste grandezze.

Abbiamo facilmente convenuto che, per esempio, la lunghezza del filo non dipende dal peso, né tantomeno il contrario. (abbiamo escluso di usare un filo elastico).

Non sapevamo invece se il tempo di oscillazione variasse in funzione del peso, della lunghezza o dell’angolo di oscillazione.

Cosa abbiamo fatto?

Abbiamo misurarato il tempo di oscillazione facendo variare a piacere le altre tre grandezze, una per volta. (Per oscillazione si intende il ritorno del pendolo nella precedente identica condizione, identica anche per il verso del suo moto)

Abbiamo capito che l’errore del “cronometrista” è inevitabile (nessuno è perfetto) e per quanto piccolo, è molto importante rispetto ad un tempo di oscillazione di uno o due secondi e abbiamo risolto il problema suddividendo l’errore su 10 oscillazioni

Ogni gruppo era composto da un cronometrista e un “contatore”; quest’ultimo contava via via   le dieci oscillazioni complete, lavorando in tandem con il primo. Ovviamente per ottenere il tempo di oscillazione è stato sufficiente dividere per 10 il tempo rilevato e in questo modo si divide anche l’inevitabile errore, che diventa trascurabile.

Per angolo di oscillazione intendiamo quello tra la verticale e il filo del pendolo nel punto morto di partenza. (In realtà questo angolo diminuisce leggermente durante le 10 oscillazioni che l’esperimento richiede, ma non possiamo porci alcun rimedio, il moto perpetuo non esiste…)

Abbiamo riportato le varie coppie di valori (almeno 4, consigliate 6) su tre tabelle e poi su tre grafici cartesiani, ponendo come x (variabile indipendente) prima il peso, poi l'angolo, poi la lunghezza e come y (variabile dipendente) il tempo.

In un secondo momento abbiamo rappresentato sul grafico cartesiano la funzione della legge del pendolo

e l'abbiamo confrontata con il nostro grafico  lunghezza-tempo.... COINCIDE !!!!

NUMERI AMICI, PERFETTI, FIDANZATI, FELICI

Un giorno chiesero a Pitagora: "Chi è un amico?"
Egli rispose: "Colui che è l'altro me stesso."
E portò come esempio i numeri 220 e 284. Sono due numeri amici perché ciascuno di essi è uguale alla somma dei divisori propri dell'altro.
Un divisore proprio di un numero è un divisore minore del numero stesso.
I divisori di 220 sono 1,2,4,5,10,11,20,22,44,55,110
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
I divisori di 284 sono 1,2,4,71,142
1 + 2 + 4 +71 + 142 = 220
I numeri  200 e 284 sono la più piccola coppia di numeri amici.

Da un racconto di Titu Andreescu, Illinois Mathematics and Science Academy.

Il sultano e il matematico

C'era una volta un sultano che si considerava un grande solutore di problemi.
Le guardie gli dissero che uno dei suoi prigionieri era un matematico.
Il giorno seguente il sultano andò a far visita al prigioniero e gli lanciò la sfida seguente:
"Puoi scegliere se rimanere in prigione per tutta la vita o darmi un problema da risolvere. Ma deve essere un problema veramente difficile perché ti lascerò libero finché non troverò la soluzione, ma appena avrò trovato la soluzione ti farò tagliare la testa."
Il prigioniero accettò la sfida senza esitazione.
Diede al sultano il seguente problema:
"La somma di tutti i divisori di 200, escluso il numero stesso, è:
1 + 2 + 4 + 5 + 10 + 11 + 20 + 22 + 44 + 55 + 110 = 284
e la somma di tutti i divisori di 284, escluso il numero stesso, è:
1 + 2 + 4 +71 + 142 = 220.
Trova un'altra coppia di numeri come questi."
Il prigioniero di questa storia se ne andò libero e morì a tarda età con la testa sul collo perché il sultano non fu mai capace di risolvere il problema che egli gli diede.


La coppia di numeri amici (17.296 ; 18.416), spesso attribuita a Fermat (Beaumont-de-Lomagne, 17 agosto 1601 – Castres, 12 gennaio 1665), in realtà è stata scoperta dall'arabo al-Banna nel XIII secolo.
La coppia (9.363.584; 9.437.056) fu scoperta da Descartes.
Il mitico Euler (Basilea, 15 aprile 1707 – San Pietroburgo, 18 settembre 1783), è stato un matematico e fisico svizzero.scoprì ben 59 coppie di numeri amici.
Thabit ibn Qurra scoprì una formula per calcolare coppie di numeri amici.
Se si riesce a trovare un numero n che rende primi i numeri a,b,c delle espressioni seguenti:
a = 3 × 2^n - 1
b = 3 × 2^n-1 - 1
c = 9 × 2 ^(2n-1) - 1
allora i due numeri
2n × a × b
2n × c
sono amici.
Per n=2 si ottiene la coppia 220, 284, per n=4 si ottiene la coppia  17.296, 18.416, per n=7si ottiene 9.363.584 and 9.437.056, rispettivamente le coppie di Pitagora, al-Banna e Descartes.
Tra 0 e 100.000.000 esistono 236 coppie di numeri amici.

Se un numero è amicabile di se stesso, cioè se la somma dei suoi divisori (escluso il numero stesso) è euguale a se stesso (come il numero 28), è chiamato "numero perfetto".


Si dicono “numeri fidanzati” due numeri per i quali  la somma dei divisori di un numero (uno escluso) è uguale all’altro numero. Sono fidanzati i numeri 48 e 75. Infatti, i divisori di 48 sono 2, 3, 4, 6, 8, 12, 16, 24; la loro somma è 75; i divisori di 75 sono 3, 5, 15, 25; la loro somma è 48.

Si prende un numero, si elevano al quadrato le sue cifre e si sommano i risultati, quindi si ripete l'operazione con il numero ottenuto. Se dopo un po’ di passaggi si raggiunge il numero 1, il numero di partenza è detto “numero felice”. 19 è un numero felice, perché 1+81=82; 64+4=68; 36+64=100; 1+0+0=1.

Ecco qui una applet per trovare alcuni numeri amicali , per numeri non più grandi di 50000

NUMERI PRIMI DI MERSENNE

Da http://ilblogdigianni.altervista.org/i-numeri-primi-di-mersenne/ 

                                            I Numeri Primi di Mersenne

M.Mersenne

                                                    Cosa sono i numeri primi di Mersenne?

Un numero primo di Mersenne è un numero primo esprimibile come:

con “n” intero positivo primo.

I numeri primi di Mersenne prendono il nome da Marin Mersenne, nato l’8 settembre 1588 a Oizé, è stato un matematico, teologo e filosofo, noto principalmente per i cosiddetti numeri di Mersenne. Si dedicò anche alle riedizioni dei trattati di Euclide, Archimede ed altri matematici greci. Grazie alle sue corrispondenze con le principali personalità scientifiche e matematiche dell’epoca, Mersenne fu un attivo divulgatore del pensiero matematico del suo tempo.

Mersenne morì a Parigi il 1 settembre 1648 a causa di complicazioni seguite ad un intervento chirurgico.

Un numero primo è un numero intero divisibile esclusivamente per uno e per se stesso. Per costruire i numeri primi di Mersenne bisogna partire dai numeri primi e poi applicare una semplice formula. Quelli che si ottengono sono però dei semplici numeri di Mersenne, non è detto siano primi. Quindi alla fine bisogna verificare che siano effettivamente primi. Considerando i numeri primi più piccoli: 2, 3, 5, 7, 11, 13, ecc.

Prendendo il numero 2 e moltiplicandolo per se stesso un numero di volte pari al numero primo di riferimento (n), ottenendo quindi la potenza di 2 di grado n. Se n vale 2 si ottiene 4, se n vale 3 si ottiene 8, se n vale 5 si ottiene 32 e così via. Al risultato ottenuto si deve sottrarre uno. I numeri di Mersenne più bassi che si possono ottenere dunque sono 3, 7, 31 e 127. Ma non è detto che siano numeri primi e quindi primi di Mersenne.

Bisogna quindi infine verificare che i numeri ottenuti siano anche numeri primi. Per fare questo si deve applicare la definizione di numero primo, cioè che esso ammetta come divisore solo se stesso e uno. I più piccoli numeri di Mersenne ottenibili sono: 3, 7, 31 e 127. Ora si deve verificare quali di questi numeri sono numeri primi: provando ad analizzare i divisori puoi scoprire che i più piccoli numeri primi di Mersenne sono proprio quelli appena calcolati, in quanto sono essi stessi primi (oltre che numeri di Mersenne).

Ecco i primi 12 numeri di Mersenne.

I calcolatori hanno accelerato la scoperta dei primi di Mersenne. I primi dodici numeri primi di Mersenne sono stati scoperti prima del XX secolo. Alla fine del millennio i primi di Mersenne conosciuti erano 38; oggi invece se ne conoscono 47 e i dodici più recenti sono stati scoperti nell’ambito della GIMPS, la Great Internet Mersenne Prime Search, iniziativa che sfrutta le risorse disponibili di migliaia di computer in rete per cercare i primi di Mersenne. Il più grande numero primo conosciuto (a settembre 2008) è proprio un numero di Mersenne trovato nell’ambito della GIMPS; scritto in base dieci è un numero di 12.978.189 cifre, precisamente:

                                                    

LA CELLULA PIU' GRANDE E'........

Qual è la cellula più grande della Terra?

Generalmente si pensa che la cellula più voluminosa sia l’uovo di struzzo che è grande all’incirca quanto una palla da tennis. In realtà, vince la gara l’alga  del genere Caulerpa, anch’essa costituita da un’unica cellula. C. taxifolia é un’alga verde tipica dei mari tropicali, dove la temperatura media dell’acqua non scende mai al di sotto dei 20° C. L’analogia con le foglie del tasso ne giustifica il nome; solitamente le fronde non superano i 15 cm. Nel Mediterraneo tale specie è affetta da gigantismo, nel senso che le fronde possono superare anche i 40 cm! Al genere Caulerpa appartengono 73 specie differenti, costituite da una lunga base orizzontale da cui si dipartono “radici”, verso il basso, e uno “stelo” provvisto di “foglie” verso l’alto. Si tratta tuttavia  di una sola cellula plurinucleata. Nel corso del suo accrescimento si suddividono solo i nuclei, ma questa divisione non interessa la membrana cellulare. Si tratta dunque, per quanto se ne sa fino a oggi, della cellula più grande del mondo. 

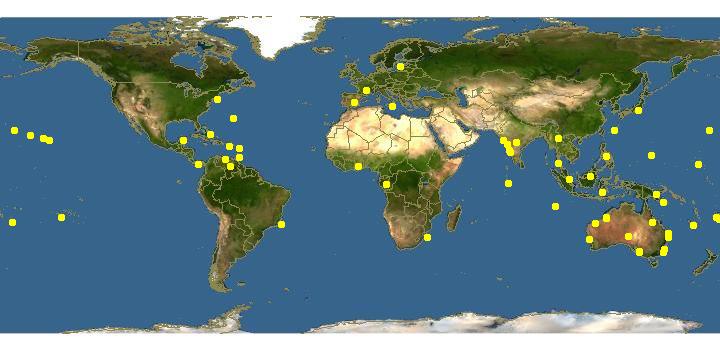La sua storia nel Mediterraneo inizia intorno agli anni ‘50. In quel periodo gli acquari pubblici d’Europa importavano diverse specie di Caulerpa a scopi decorativi. Negli anni ‘70 Caulerpa taxifolia venne acquistata per la prima volta dall’acquario di Stoccarda e presto distribuita ad altri acquari: tale alga infatti, oltre ad essere caratterizzata da un bel colore verde acceso, è molto resistente, ricopre velocemente il fondo delle vasche ed è un ottimo rifugio per le specie criptiche, caratteristiche che decretarono il suo successo. Nel 1983 fa il suo arrivo all’Acquario di Monaco e nel 1984 si ha la prima segnalazione in mare, proprio ai piedi dell’Acquario del Principato. Subito non ci fu alcun segno di allarmismo: una specie tropicale non sarebbe mai stata in grado di superare il "rigido" inverno mediterraneo! Invece nel 1989 aveva ricoperto 10.000 m2 di fondale! Nel 1990 venne segnalata a Cap Martin per un ricoprimento totale di 30.000 m2. Alla fine del 1996 le segnalazioni rinvenute consentirono di stimare una superficie di ricoprimento pari a circa 30.000.000 di m2. Oltre al Principato di Monaco, i principali paesi coinvolti nel fenomeno sono Francia, Spagna, Italia e Croazia.

Questa alga è conosciuta come alga Killer a causa delle tossine che produce, nocive anche per l'uomo.

Essa è in grado di colonizzare qualsiasi tipo di substrato a danno delle altre alghe e non viene assolutamente danneggiata dalle acque inquinate. Un' ulteriore differenza tra la "sorella" tropicale e quella mediterranea risiede nella strategia riproduttiva: contrariamente a tutte le altre alghe verdi, la nostra C. taxifolia si riproduce anche asessualmente.

Vediamo qui come è fatto un uovo

ANGOLI ESTERNI DI UN POLIGONO

Ecco qui l'applet di geogebra che abbiamo visto in classe, riguardante la somma degli angoli esterni di un poligono qualsiasi. Vi metto anche il collegamento al blog da cui l'ho tratta: "Sinapsi delle idee" .

NUMERI PRIMI E CRITTOGRAFIA

Da quando esiste la matematica, si è cercata una regola  che permetta di individuare i numeri primi, cioè quei numeri che sono divisibili soltanto per se stessi e per 1. 

Il grande matematico tedesco Georg Bernhard Riemann nel 1859 introdusse una funzione ( una formula), da allora nota come “zeta di Riemann”, che – si suppone – permette di individuare tutti i numeri primi.

Non si tratta di cosa da poco. E’ noto che esistono infiniti numeri primi, ma capire se un numero è primo o meno può portare via molto tempo. Se il numero è molto elevato, l’impresa è ardua anche per un computer.

La validità della funzione zeta di Riemann è stata verificata per un miliardo e mezzo di casi; ma ciò non rappresenta una dimostrazione della sua validità in generale.

Ci ha provato  anche John Nash, il matematico impersonato da Russell Crowe nel film “A beautiful mind”. 

E’ ormai da trent’anni che John Nash (nato nel 1924, premiato con il Nobel per l’economia nel ’94) convive con una forma grave di schizofrenia, forse dovuta allo sforzo mentale.

Per un matematico trovare la dimostrazione dell’ipotesi di Riemann varrebbe più di tutto l’oro del mondo, ma, anche da un punto di vista venale, un tale risultato varrebbe ben più del milione di dollari messo in palio dal Clay Mathematics Institute. 

Il mondo dei numeri primi è ancora largamente inesplorato. Per questo, e per le loro proprietà matematiche, i numeri primi sono la base di un ampio insieme di codici, in particolare dei codici in uso nell’era di Internet. Chi riuscisse a dimostrare l’ipotesi di Riemann otterrebbe la piena conoscenza di quel mondo, e dunque la capacità di poter violare i codici elettronici.

Erano gli anni ’70 quando tre ricercatori del MIT – Ron Rivest, Adi Shamir e Leonard Adleman – svilupparono l’algoritmo che, a partire dal nuovo millennio, costituisce la base dei cifrari che proteggono la riservatezza dei numeri delle carte di credito, e in generale di qualunque password di accesso online. Il codice si basa sulla scelta di due numeri primi, che ne rappresentano le chiavi; più alti sono, più il codice è sicuro. Il messaggio cifrato che viaggia sul Web, per esempio dalla banca al cliente,è legato al prodotto di quei due numeri; ma risalire, dal prodotto, ai due numeri che l’hanno generato, e quindi violare il codice, è praticamente impossibile, anche per il più potente dei computer.

Per farsi un’idea: in un esperimento effettuato nel 2005, un supercomputer il cui sistema di calcolo radunava la potenza di ottanta processori da 2,2 Giga Hertz impiegò cinque mesi per trovare due divisori primi di un numero di 193 cifre. I numeri utilizzati nella cifratura RSA (così chiamata dalle iniziali dei suoi inventori) sono costituiti, di regola, da trecento cifre decimali.

La cifratura RSA sta rapidamente diventando la protezione standard dei dati ultrasensibili in ambiente internet. Si basa sull’assunto secondo cui fattorizzare un numero molto grande (cioè, trovare tutti i numeri primi che lo dividono) è un’operazione impraticabile da un punto di vista computazionale. Ciò è senz’altro vero allo stato attuale delle conoscenze, ma la ricerca va avanti.

Se venisse dimostrata l’ipotesi di Riemann, se i numeri primi uscissero dal mistero in cui sono avvolti, chissà... Crollerebbe Wall Street? Sprofonderebbe il Nasdaq? 

 “Il mondo degli affari non ha mai prestato tanta attenzione come oggi a quanto accade sulle lavagne dei matematici puri”.

Vedi qui sotto un ulteriore  esempio di codici con doppia chiave.

Ogni utilizzatore si crea la propria coppia di chiavi; la chiave privata viene tenuta segreta e non viene mai rivelata a nessuno (nemmeno alle persone con le quali si comunica); viceversa, la chiave pubblica viene diffusa in vari modi, per esempio depositata in archivi pubblici (keyserver) a disposizione di chi la desideri. È importante che la chiave pubblica sia liberamente accessibile, perché chiunque voglia comunicare con la persona che l'ha generata dovrà preventivamente munirsi di questa, con la quale cifrerà il messaggio da inviargli.

LE CELLULE ANIMALI : COME SONO FATTE

In ogni cellula è possibile distinguere 3 parti ben differenziate:

• la membrana cellulare che riveste la cellula, ma lascia penetrare le sostanze nutritive ed espellere quelle di rifiuto;
• il citoplasma, una sostanza gelatinosa che contiene vari organuli, importanti per la vita della cellula;
• il nucleo, minuscolo corpuscolo quasi sempre al centro della cellula e separato dal citoplasma per mezzo della membrana nucleare. Il nucleo è il centro di comando della cellula ed in esso è racchiuso il segreto della vita: i cromosomi, che custodiscono i geni, cioè i responsabili dell'ereditarietà biologica, che fa sì che i figli assomiglino ai genitori.

Nel citoplasma "galleggiano" vari organuli, ognuno dei quali svolge una funzione.

• i ribosomi, che elaborano le proteine;
• il reticolo endoplasmatico, che contiene buona parte dei ribosomi;
• l'Apparato del Golgi, sacche che raccolgono e distribuiscono le sostanze prodotte dalla cellula;
• i mitocondri, vere centrali energetiche, che producono energia dalle sostanze nutritive, attraverso un processo chiamato respirazione cellulare;
• i lisosomi, vacuoli particolari che contengono enzimi che digeriscono le sostanze nutritive;
• i vacuoli, contenenti le sostanze di riserva.

Da http://www.pianetascuola.it/risorse/media/secondaria_secondo/scienze_natura/labonline/04/files/esplora.htm un'attività sugli esseri viventi

orecchiette o cellule?

Ma quanto è grande una cellula?

Un micron è la milionesima parte del metro
Il nanometro è la miliardesima parte del metro